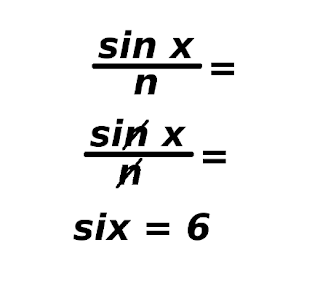Stillness.

22 November 2009. 615pm. Today, I simply long for stillness.

The Missing Peso

This paradox probably has thousands of variants already. Since the concept is no longer original, I will reinvent the presentation by introducing one of my favorite comfort foods: yogurt!

~o~o~

After watching a rather depressing film, three friends decided to share a yogurt which costs PhP 145. Each one of them gave the cashier a 50-bill. In return, the cashier hands them five 1-peso coins as change. Each of them takes one of the coins and deposits the remaining two coins in the tip box. When seated, one of the girls did a simple math. Each girl's share is PhP 49, giving a total of PhP 147 for the three of them. Add the PhP 2 tip to this gives only a total of PhP 149. Where is the other 1-peso? Explain this paradox.

~o~o~

The problem was presented in a way the readers would think that there is a missing peso, when in fact what is really missing is logic. In truth, the transaction is balanced; think of inflow-outflow, or cash flow analysis. The yoghurt costs PhP 145; 1 peso was returned to each of them for a total of 3 pesos; they dropped 2 pesos on the tip box. The sum of these amounts is PhP 150. Equivalently, each of them contributed only PhP 49 giving a total of PhP 147 and the yoghurt plus the tip equals PhP 147. Thus, every peso has been attributed for.

By the way, the yogurt is worth fighting the missing peso for! Visit Red Mango for proof.

[Photo from Red Mango Philippines Facebook]

Funny Maths

After a day of chanting formulas in my head, solving exam problems and finishing up a proposal due today, I sensed a migraine coming. Fortunately, these jokes saved me from chugging down a painkiller or two and restored my sanity. Laughter is no doubt the best medicine! Photos taken from http://www.tanyakhovanova.com/Jokes/pictures.html.

A-Kira-and-Kevin Problem

This is one of those Kira and Kevin problems found in the Exam MLC Actuarial Models. This particular question really pissed me off the first time I tried it because it took me a looong time to solve. This is easy though, if you are familiar with the concept of a joint-life status.

Kevin and Kira excel at the newest video game at the local arcade, "Reversion". The arcade has only one station for it. Kevin is playing. Kira is next in line. You are given:

1. Kevin will play until his parents call him to come home.
2. Kira will leave when her parents call her. She will start playing as soon as Kevin leaves if he is called first.
3. Each child is subject to a constant force of being called: 0.7 per hour for Kevin; 0.6 per hour for Kira.
4. Calls are independent.
5. If Kira gets to play, she will score points at a rate of 100,000 per hour.

Calculate the expected number of points Kira will score before she leaves.

Random POVs Vol3

The rain.

The metal is cold against my palm.
A degree colder than the
Pencil-scrawled sheet before me.
My equations danced across the page
Mocking me the entire time.
I raised my chin in defiance.

I made a mistake somewhere
But exactly where, I ain’t sure.
I chanted the Balducci assumptions again one by one
Praying, cursing and rebuking myself all the while.
I punched the numbers on the metal again.
Midway, I could foresee a 3-digit difference.
I stopped, closed my eyes for a minute
And looked outside.
It is getting darker.

I am distracted, this you hinted one time.
I suddenly had the urge to call you.
Whew.
The rain pounded heavily on the roof.
And lightning sliced the sky.
I knew I am done for the day.
But the call has to wait.

A Birthday Song.

I wish you all the best life has to offer.
I wish you happiness and abundance.
I wish for the realization of your dreams.
I wish you a great career and a wonderful family.
I wish that your ideals may not fail you.

In moments of challenges…
Take courage from the truth and inspiration from love.
And more importantly, rejoice!

In times of discouragement…
Remember us, the people whose lives you have touched.
Then, rejoice!

In times of persecution and discrimination…
Remember that the spirit of a warrior can never be broken whilst
The genius of the man can never be overpowered;
That what they say doesn’t matter as much as what you say to yourself,
And that they are only inggit , duh!
And, rejoice! Remember that we postulate that we are beautiful!

In times of solitude…
Have faith that we are always there to share your loneliness and pain,
That we are just a click of a mouse away.
Still, rejoice! For it is in times of solitude that we hear our hearts speak.

In times of achievement and glory…
Believe us when we say, we never doubted you,
That credit eventually fell where it is due;
That we celebrate with you your triumph and happiness,
With champagne or beer, and grins plastered on our faces.
And more so, rejoice!

Happy Birthday, MaFia!

Random POVs Vol2

The coffee.

The third time I read the sentence
I knew it was futile.
My eyes hurt as much as my brain.
I looked at you again.

Even against the darkness,
I noticed the slight crease of your brows
And the mirth on your lips
As you read through the lines.

You paused, looked back
And typed furiously.
I flipped the magazine in my hands.
Funny, I can’t remember what her name is
But I know she gets paid 5000 an hour.
Numbers do really amaze me more than words.

My gaze went back to you again.
The fifth in ten minutes.
I am grateful that Shang has a joke for a generator
This way I get to observe you as boldly as I can.

I saw you squint at the page.
You used to do that when you were thinking.
Now, it could be the light.
Silently, I wondered
What else changed in 5 years?

I traced the contours of your face with my eyes
My gaze lingered at your lips.
You still are beautiful.
I emptied what’s left of my cup
And hoped that that went unnoticed.

I raised my eyes again
Only to find amusement in yours.
Uh-oh, busted.

Random POVs Vol1

The wait.

The cursor stares back at me.
Sigh.
This ain’t easy for me too,
I shouted back more for me against its angry glare.
I wonder why it is so stubborn
For when you think about it
This is confusing me a lot more.

5 minutes passed
And I can’t write a single word.
Surely, I should have forgotten, right?
Wrong.
It was 5 years now
But the pain is as fresh as newly-cut wound.
Now, why is this a good idea again?
Indeed, this is confusing me a lot more.

Just 5 minutes more
And I ready myself to bolt out the door.
I wonder why I would have to brave this wait
Not when I need to be just scared shitless.
The cursor blinks back again
And I stared just as angrily.
I finished my tea
And stood.
Maybe there won’t be any words coming…

5 steps.
A “hi” then a smile.
Thank heavens, I am wrong.

Believe

I wrote this one when I was beginning to get too comfortable with teaching that I wanted to forego my graduate studies in UP. Unconsciously, I was building a comfort zone. I would justify to myself that taking a masters degree in Cebu while teaching 8 math subjects to an average of 480 students a week, is the selfless and most responsible thing to do. No matter how I justify it though, it all simplifies to one thing: I was scared shitless. I was scared of failure. I have wanted to study in UP since I was in high school and was afraid that I might realize that I was never good enough for my dreams. However, when it reached the point that I was slowly complying with the requirements of a graduate school in Cebu, alarm bells went off. And selflessness be damned. I ripped off the page where this poem was written, kept it in my pocket and decided to fly to Manila right after summer classes was over. I guess it was just appropriate that the last class I taught that summer was Mathematical Logic.

That was almost five years ago. I finished my masters degree already, passed SOA exams but can't seem to find the work I want. I am scared again; plus maybe, a little bored, depressed and hopeless. Pretty strong feelings, right? Yep, and negative and useless because when totalled, I am still jobless. I guess it's about time that I start believing again.

~0~0~

Move in tune

with the song

of the earth.

Dance with the

tulips and let

the sun admire

your grace

and the moon envy

your youth.

Believe Mae and

the wind, earth,

water and fire

will conspire with you,

with your dreams...

Of Techniques...

These three problems were presented during the Area Stage Competition of the 10th Philippine Mathematical Olympiad. On the average, each of them requires only a few minutes to solve, so if you find yourself working on one way too long, change techniques.

If 2A99561 is equal to the product when 3(523+A) is multiplied by itself, find the digit A.

The perimeter of a square inscribed in a circle is p. What is the area of the square that circumscibes the circle?

The sum of the first ten terms of an arithmetic sequence is 160. The sum of the next ten terms of the sequence is 340. What is the first term of the sequence?

Apples and Alex

OMG! When I read in yahoo news that Stephanie March will guest star in Law and Order: Special Victims Unit for six episodes, I squealed, shrieked and cussed! It's about damn time that they bring back the kick-ass Alexandra Cabot in the fold. Let's admit it, ADAs Casey Novak and Kim Greylek are not half as good as Cabot; hell, not even a quarter as good! They can and never will, fill in Cabot's shoes. Novak realized this early on and I bet Greylek will too, sooner or later. Or maybe she does already; I wouldn't know, I boycotted the show. I mean, I wasn't following every episode as religiously as I used to. I guess people will remember Novak as the ADA who replaced Alex Cabot and Greylek as the someone who replaced a replacement. What can I say? Cabot completes SVU; she sets the bar. Even the ratings are proof enough and numbers don't lie. It literally swan-dived after she was forced into Witness Protection Program. So after hearing that she will return for six episodes I am grinning rather widely it hurts! I guess saying that I am excited is honestly an understatement.

Ok, moving on. The problem below merits posting simply because we encounter it way too often. Well that, and the fact that I can't find the list of math problems I compiled a long time ago. Anyway, this problem illustrates the use of the technique known as working backwards. Read and try solving it and you will know what I mean. I can't help it, I just have to name the character, Alex.

Alex bought a bag of apples on Monday and she ate a third of them. On Tuesday, she ate half of the remaining apples. On Wednesday when she looked inside the bag, she found that she had only two apples left. How many apples did she have at the start?

Buddha in Glory

No, this is not a math problem. Yes, this is a poem and one of my favorites. Buddha in Glory is one of the greatest tribute to self-exaltation. What inspires me is the fact that the poem affirms the endless and continuous possibilities present to an enlightened man.

Buddha in Glory

by Rainer Maria Rilke

Center of all centers, core of cores,

almond self-enclosed, and growing sweet--

all this universe, to the furthest stars

all beyond them, is your flesh, your fruit.

Now you feel how nothing clings to you;

your vast shell reaches into endless space,

and there the rich, thick fluids, rise and flow.

Illuminated in your infinite peace,

a billion stars go spinning through the night,

blazing high above your head.

But in you is the presence that

will be, when all the stars are dead.

For J

The first time I read this problem it was my second-year in high school, a time when PhP20 can buy a lot and the Backstreet Boys mania thick in the air. The most recent time I encountered this problem was more than ten years hence, when I was reviewing for SOA Exam P and performing the statistical treatment for J’s thesis. In one of our discussions, J commented that it is impossible to determine whether a student who had identified the correct answer in a multiple-choice question really knew the answer and was not simply guessing. True, we can't say so with 100% certainty. But with certain assumptions, it is not completely insolvable either. The problem below illustrates this.

In answering a question to a multiple-choice test, a student either knows the answer or guesses. Let p be the probability that the student knows the answer and 1-p be the probability that the student guesses. Assume that the student who guesses the answer will be correct with probability 1/m, where m is the number of choices. What is the conditional probability that the student knew the answer to a question given that he had answered it correctly?

The answer is given by

We illustrate this with an example. Suppose you gave a multiple-choice exam with five possible choices. Student A whom you believed to have a 10% chance of knowing the correct answer for a particular question was able to identify the correct answer. The expression above tells us that the probability that Student A really knew the answer and was not simply doing "eeny, meeny, miy, moe" given that he has answered correctly is 5/14. In other words, the probability that Student A was just lucky is 9/14.

The Monty Hall Problem

The Monty Hall problem appeared on the movie 21, a film from Columbia pictures inspired by the story of the MIT Blackjack Team. During an advanced class, Professor Micky Rosa, played by Kevin Spacey, challenged Ben Campbell, played by Jim Sturgess, with the Monty Hall paradox which Campbell solves successfully. This meeting eventually led to Campbell joining the blackjack team headed by Rosa. Together with four other MIT students, the team went to sweep Vegas' casinos by storm using card counting. Below is a version of the Monty Hall problem as it appears on the book, Introduction to Mathematical Statistics (6th ed.) by Hogg, McKean and Craig.

Suppose that there are three curtains. Behind one of the curtains is a nice prize while behind the other two are worthless prizes. A contestant selects one curtain at random, and then Monty Hall opens one of the other two curtains to reveal a worthless prize. Hall then expresses the willingness to trade the curtain the contestant has chosen for the other curtain that has not been opened. Should the contestant switch curtains or stick with the one she has? What is the probability that he wins the prize if he switches?

To answer the first question, we only need to know the probability that the contestant wins the prize should he change curtains. Using the Law of Total Probability, this is given to be 2/3. This means that the odds in favor of the event, winning after switching curtains, is 2:1. Thus, it is advisable that the contestant switches.

Chapter 0

Q.E.D. is an abbreviation of the Latin phrase quod erat demonstrandum which literally translates to, that which was to be demonstrated. This is one of the oldest and most commonly used symbols displayed at the end of a mathematical proof or argument to indicate its completion. Other symbols include a solid square, a sharp, which I used throughout high school, and even the innovative letters, H.N.G., which means "human na gyud".

This blog will mostly contain some of the math problems that have sparked my interest at one time or another and will resemble the math calendar found in the Mathematics Teacher journal. I have no idea how to post the solutions just yet so if you want a copy, you may email me. I might also post some problems which I haven't solved, but they will be identified accordingly. Hopefully, this blog would push me to realize a compilation of math problems that I have been planning to work on.

I invite you to read on and recall your algebra, trigonometry, geometry, probability, calculus and other tricks, but unlike high school, have some fun (if possible). Prove, re-solve the problems in your own way (with or without listing the GIVEN, as probably required before), enjoy or simply be confused. Well, what can I say? One problem a day keeps the boredom away!